大话数据结构（一）：那些年面试常见的 Java 排序算法

发表于 | 分类于 | 评论数： | 阅读次数：
本文字数统计： 7.9k | 阅读时长 ≈ 7 分钟

前言

排序就是将一组对象按照某种逻辑顺序重新排列的过程。排序在数据处理和现代科学计算中有很重要的地位，应用于很多领域。排序问题一直是程序员工作与面试的重点，今天特意整理研究下与大家共勉。本文将介绍一下常见的排序算法以及 Java 代码实现，如有问题，欢迎指正！

各算法原理及代码实现

1556538098111

冒泡排序（Bubble Sort）

冒泡排序（Bubble Sort）是一种简单的排序算法。它重复地走访要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢 “浮” 到数列的顶端。

原理

  • 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  • 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
  • 针对所有的元素重复以上的步骤，除了最后一个。
  • 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

15565238194673

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
public static void bubbleSort(int[] numbers) {
    for (int i = 0; i < numbers.length - 1; i++) {
        for (int j = 0; j < numbers.length - i - 1; j++) {
            if (numbers[j] < numbers[j + 1]) {
                // 交换两数位置
                int temp = numbers[j];
                numbers[j] = numbers[j + 1];
                numbers[j + 1] = temp;
            }
        }
    }
}

快速排序（Quick Sort）

选择一个基准元素，通常选择第一个元素或者最后一个元素，通过一趟扫描，将待排序列分成两部分，一部分比基准元素小，一部分大于等于基准元素，此时基准元素在其排好序后的正确位置，然后再用同样的方法递归地排序划分的两部分。

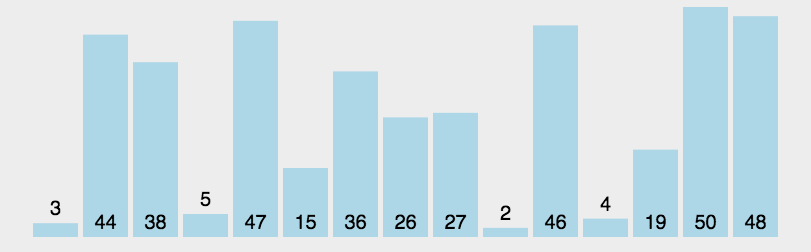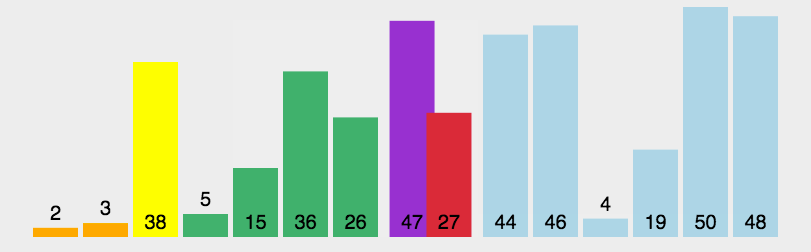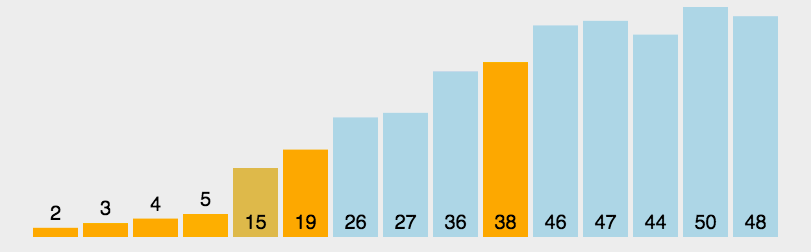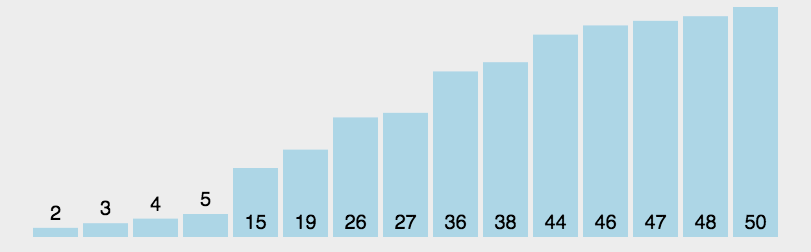
15565242837841

快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static void quickSort(int[] numbers, int low, int high) {
    // 找到递归算法的出口
    if (low >= high) {
        return;
    }

    int temp = numbers[low], begin = low, end = high;
    while (low < high) {
        while (low < high && numbers[high] >= temp) {
            high--;
        }
        // 比中轴小的记录移到低端
        numbers[low] = numbers[high];
        while (low < high && numbers[low] <= temp) {
            low++;
        }
        // 比中轴大的记录移到高端
        numbers[high] = numbers[low];
    }
    // 中轴记录到尾
    numbers[low] = temp;

    // 对低字段表进行递归排序
    quickSort(numbers, begin, low - 1);
    // 对高字段表进行递归排序
    quickSort(numbers, high + 1, end);
}

三向切分快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public static void quickSort3Way(int[] numbers, int low, int high) {
    if (low >= high) {
        return;
    }

    int temp = numbers[low], begin = low, i = low + 1, end = high;
    while (i <= high) {
        if (numbers[i] < temp) {
            int t = numbers[i];
            numbers[i] = numbers[low];
            numbers[low] = t;
            i++;
            low++;
        } else if (numbers[i] > temp) {
            int t = numbers[i];
            numbers[i] = numbers[high];
            numbers[high] = t;
            high--;
        } else {
            i++;
        }
    }

    quickSort3Way(numbers, begin, low - 1);
    quickSort3Way(numbers, high + 1, end);
}

选择排序（Selection Sort）

直接选择排序是一种简单直观的排序算法。它的工作原理如下：首先在未排序序列中找到最小元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小元素，然后放到排序序列末尾(目前已被排序的序列)。以此类推，直到所有元素均排序完毕。

原理

假设数据放在一个数组 a 中，且数组的长度是 N，则直接选择排序的流程为：

  • 从 a[0]-a[N-1]中选出最小的数据，然后与 a[0]交换位置
  • 从 a[1]-a[N-1]中选出最小的数据，然后与 a[1]交换位置（第 1 步结束后 a[0]就是 N 个数的最小值）
  • 从 a[2]-a[N-1]中选出最小的数据，然后与 a[2]交换位置（第 2 步结束后 a[1]就是 N-1 个数的最小值）
  • 以此类推，N-1 次排序后，待排数据就已经按照从小到大的顺序排列了。

15565245438056

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public static void selectionSort(int[] numbers) {
    for (int i = 0; i < numbers.length - 1; i++) {
        // 待确定的位置
        int k = i;
        // 选择出应该在第 i 个位置的数
        for (int j = i; j < numbers.length; j++) {
            if (numbers[j] < numbers[k]) {
                k = j;
            }
        }
        // 在内层循环结束, 也就是找到本轮循环的最小的数以后, 再进行交换
        if (k != i) {
            int temp = numbers[i];
            numbers[i] = numbers[k];
            numbers[k] = temp;
        }

    }
}

堆排序（Heap Sort）

堆排序算法和直接选择排序算法最大的不同在于，堆排序算法充分利用大顶堆和完全二叉树的性质，保留每次排序后的结构，同时由于每次比较只是比较根节点和它的子节点，因此大大降低了比较的次数和交换的次数，从而提高效率。

原理

假设数据放在一个数组 a 中，且数组的长度是 N：

  • 以数组 a 为数据，建立一个大顶堆（这样对于二叉树的每个节点，根节点总是比子节点大，其实没必要要求二叉树的每个子树也是大顶堆）
  • 交换大顶堆的根节点和数组 a 中的最后一个节点（最后一个节点不在参与后边的工作）
  • 重复上边的工作，经过 N-1 次后，数组 a 已经排好序。

15565248890502

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public static void heapSort(int[] numbers) {
    // 将待排序的序列构建成一个大顶堆
    for (int i = numbers.length / 2 - 1; i >= 0; i--) { 
        // 从第一个非叶子结点从下至上, 从右至左调整结构
        adjustHeap(numbers, i, numbers.length);
    }

    // 调整堆结构 + 交换堆顶元素与末尾元素
    for (int j = numbers.length - 1; j > 0; j--) {
        // 将堆顶记录和当前未经排序子序列的最后一个记录交换
        int temp = numbers[0];
        numbers[0] = numbers[j];
        numbers[j] = temp;
        // 重新对堆进行调整
        adjustHeap(numbers, 0, j);
    }
}

public static void adjustHeap(int[] numbers, int low, int high) {
    // 先取出当前元素 i
    int temp = numbers[low];
    // 从 low 结点的左子结点开始, 也就是 2low+1 处开始
    for (int k = low * 2 + 1; k < high; k = k * 2 + 1) {
        // 如果左子结点小于右子结点, k 指向右子结点
        if (k + 1 < high && numbers[k] < numbers[k + 1]) {
            k++;
        }
        // 如果子节点大于父节点, 将子节点值赋给父节点(不用进行交换)
        if (numbers[k] > temp) {
            numbers[low] = numbers[k];
            low = k;
        } else {
            break;
        }
    }

    // 将 temp 值放到最终的位置
    numbers[low] = temp;
}

插入排序（Insertion Sort）

插入排序是一种通过不断地把新元素插入到已排好序的数据中的排序算法，常用的插入排序算法包括直接插入排序和希尔（Shell）排序，直接插入排序实现比较简单，但是直接插入没有充分的利用已插入的数据已经排序这个事实，因此有很多针对直接插入排序改进的算法。

原理

在要排序的一组数中，假设前面 (n-1)[n>=2] 个数已经是排好顺序的，现在要把第 n 个数插到前面的有序数中，使得这 n 个数也是排好顺序的。如此反复循环，直到全部排好顺序。

也就是说，先从无序区拿第一个记录出来，它是有序的，然后把无序区中的记录一个一个插入到其中，那么插入之后是有序的，所以直到最后都是有序的。

15565246207690

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
public static void insertionSort(int[] numbers) {
    for (int i = 1; i < numbers.length; i++) {
        // 保存每次需要插入的那个数
        int temp = numbers[i];
        int j;
        // 假如 temp 比前面的值小, 则将前面的值后移
        for (j = i; j >= 1 && temp < numbers[j - 1]; j--) {
            numbers[j] = numbers[j - 1];
        }
        numbers[j] = temp;
    }
}

希尔排序（Shell Sort）

希尔排序是插入排序的一种。是针对直接插入排序算法的改进。该方法又称缩小增量排序，因 DL．Shell 于 1959 年提出而得名。

原理

先取定一个小于 n 的整数 d1 作为第 1 个增量，把文件的全部记录分成 d1 个组，所有距离为 d1 的倍数的记录放在同一个组中，在各组内进行直接插入排序；然后，取第 2 个增量 d2<d1 重复上述的分组和排序，直至所取的增量 d1=1(dt<dt-1<…<d2<d1)，即所有记录放在同一组中进行直接插入排序为止。

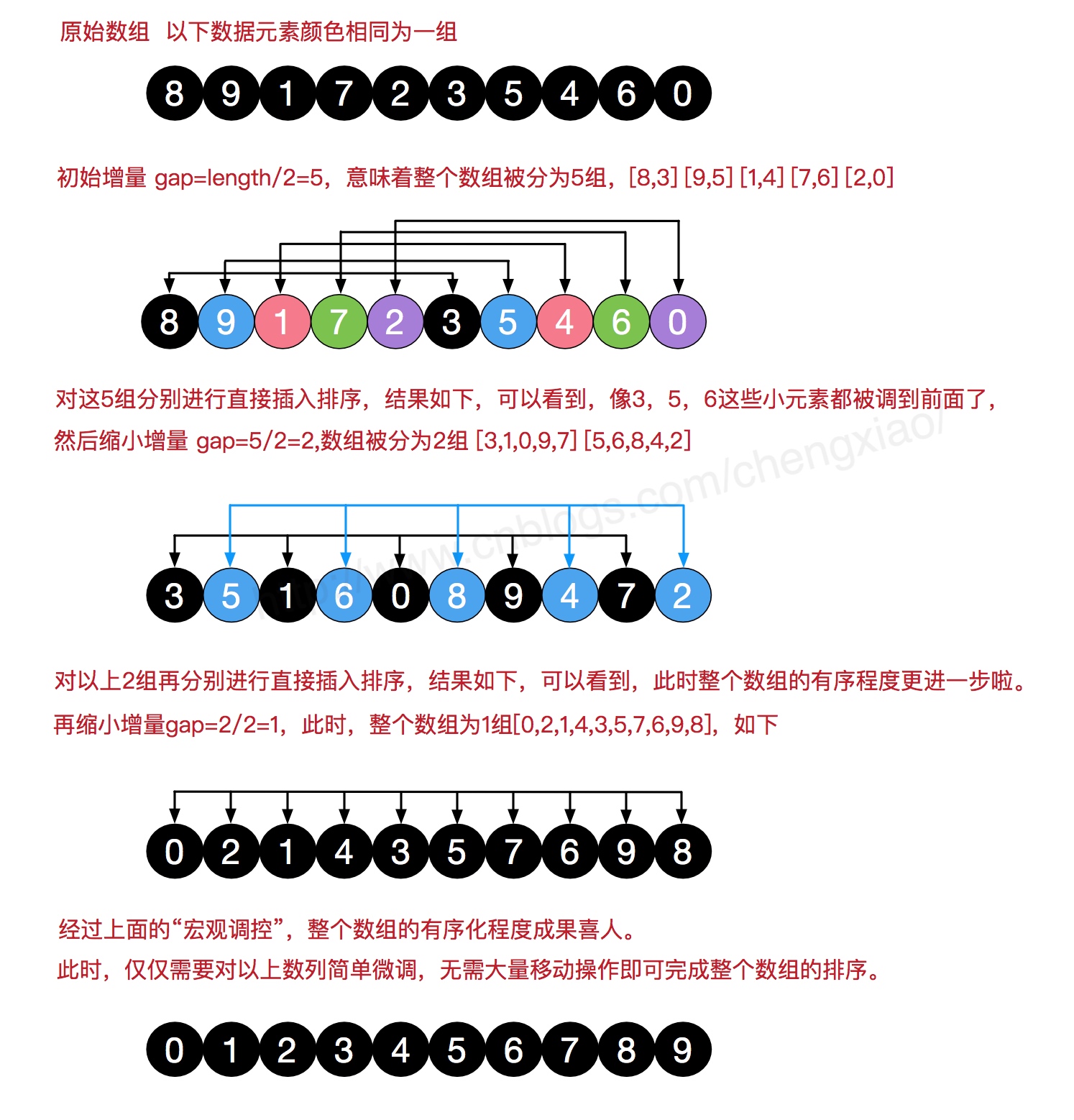
15565251647186

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static void shellSort(int[] numbers) {
    // 每次将步长缩短为原来的一半
    for (int h = numbers.length / 2; h > 0; h /= 2) {
        // 进行插入排序
        for (int i = h; i < numbers.length; i++) {
            int j;
            // 保存每次需要插入的那个数
            int temp = numbers[i];
            for (j = i; j >= h && temp < numbers[j - h]; j -= h) {
                // 如想从小到大排只需修改这里
                numbers[j] = numbers[j - h];
            }
            numbers[j] = temp;
        }
    }
}

归并排序（Merge Sort）

归并排序是建立在归并操作上的一种有效的排序算法, 该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

原理

归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

15565247200768

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public static void mergeSort(int[] numbers, int low, int high) {
    if (low < high) {
        // 找出中间索引
        int mid = (low + high) / 2;
        // 对左边数组进行递归
        mergeSort(numbers, low, mid);
        // 对右边数组进行递归
        mergeSort(numbers, mid + 1, high);
        // 合并
        merge(numbers, low, mid, high);
    }
}

public static void merge(int[] numbers, int low, int mid, int high) {
    // 申请一个新空间来保存排序后数组
    int[] mergeArr = new int[high - low + 1];
    // i、j 是检测指针, k 是存放指针
    int i = low;
    int j = mid + 1;
    int k = 0;

    while (i <= mid && j <= high) {
        if (numbers[i] < numbers[j]) {
            mergeArr[k++] = numbers[i++];
        } else {
            mergeArr[k++] = numbers[j++];
        }
    }

    // 把左边剩余的元素导入
    while (i <= mid) {
        mergeArr[k++] = numbers[i++];
    }

    // 把右边剩余的元素导入
    while (j <= high) {
        mergeArr[k++] = numbers[j++];
    }

    // 将新排好序的数组放入元素相应的位置中
    for (int m = 0; m < mergeArr.length; m++) {
        numbers[low + m] = mergeArr[m];
    }
}

大话数据结构系列

谢谢你长得那么好看，还打赏我！😘
0%